Tập phù hợp số là gì? những tập đúng theo số trong toán học tập là kỹ năng và kiến thức vô thuộc quan trọng. Dưới đây hãy cùng Bamboo tìm hiểu kiến thức về tập hòa hợp số trong toán học tập này nhé!!
Tập hợp số là gì? ví dụ về tập đúng theo số
Tập đúng theo số là 1 trong những nhóm các số nhất định. Những số này được call là phần tử của tập hợp.
Bạn đang xem: Các tập hợp trong toán học

Một vài ví dụ như về tập hòa hợp số:
Tập hợp các số trên mặt đồng hồ => các thành phần là: 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12.Tập hợp các số thoải mái và tự nhiên = > N=0; 1; 2; 3;…Tập hợp những số thoải mái và tự nhiên các số trường đoản cú 0 cho đến 99Các nhiều loại tập hòa hợp số cơ bản
Tập hợp những số tự nhiên quy mong là N
N=0, 1, 2, 3, 4, 5, ...
Tập hợp những số nguyên quy ước là Z
Z=…, -4, -3, -2, -1, 0, 1, 2, 3, 4, ….
Tập hợp số nguyên bao hàm các phân tử là những số tự nhiên và thoải mái và các thành phần đối của những số tự nhiên.
Tập hợp của các số nguyên dương kí hiệu là N*
Tập hợp các số hữu tỉ quy ước là Q
Q= a/b; a, b∈Z, b≠0
Một số hữu tỉ hoàn toàn có thể được màn biểu diễn bằng một số trong những thập phân hữu hạn hoặc số thập phân vô hạn tuần hoàn.
Tập hợp các số thực quy ước là R
Mỗi số được biểu diễn bằng một trong những thập phân vô hạn không tuần trả được ta gọi là một số vô tỉ. Tập hợp những số vô tỉ được quy mong kí hiệu là I. Tập hợp của các số thực bao hàm các số hữu tỉ và những số vô tỉ.
Mối dục tình của tập đúng theo số
N: tập hợp các số trường đoản cú nhiên
Z: tập hợp các số nguyên
Q: tập hợp các số hữu tỉ
R: tập đúng theo số thực
Mối quan hệ tình dục của bọn chúng là: N ⊂ Z ⊂ Q ⊂ R
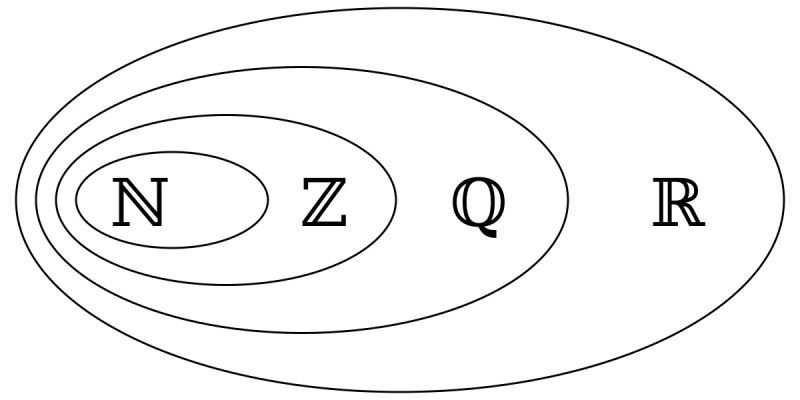
Một số tập hợp nhỏ của tập thích hợp số thực
Ví dụ a, b là 2 số thực (a Khi đó Tập hòa hợp các phần tử thuộc A hoặc thuộc B., cam kết hiệu: A∪B Tập hòa hợp các bộ phận giao cả A cùng B., ký kết hiệu:A∩B Tập đúng theo các bộ phận thuộc A dẫu vậy không nằm trong B, ký hiệu: A∖B Cho A là tập con của tập E. Phần bù của A vào X là X∖A, ký hiệu : CXA là tập đúng theo cả các phần tử của E mà không là thành phần của A. Câu 1: mang đến tập vừa lòng A = {x ∈ R | -3 B. <-3; 1>. C. <-3; 1). D. (-3; 1). Hướng dẫn: =>Chọn D. Theo lý thuyết: (a;b) = {x ∈ R | a chọn A. Bởi vì (1; 4> gồm những số thực x mà 1 A. A = <4; 9>. B. A = (4; 9>. C. A = <4; 9). D. A = (4; 9) Hướng dẫn: => chọn A. Theo lý thuyết: Câu 4: mang đến hai tập hợp A = <-2; 7); B = (1; 9>. Tra cứu A ∪ B. Xem thêm: Những Bài Hát Hàn Quốc Buồn Hay Nhất, Những Bài Hát Nhạc Phim Hàn Quốc Buồn A. (1; 7). B. <-2; 9>. C. <-2; 1). D. (7; 9>. Hướng dẫn: => chọn B. Ta trình diễn tập hòa hợp A cùng B bên trên trục số như sau:
Đoạn a cho b được ký kết hiệu là 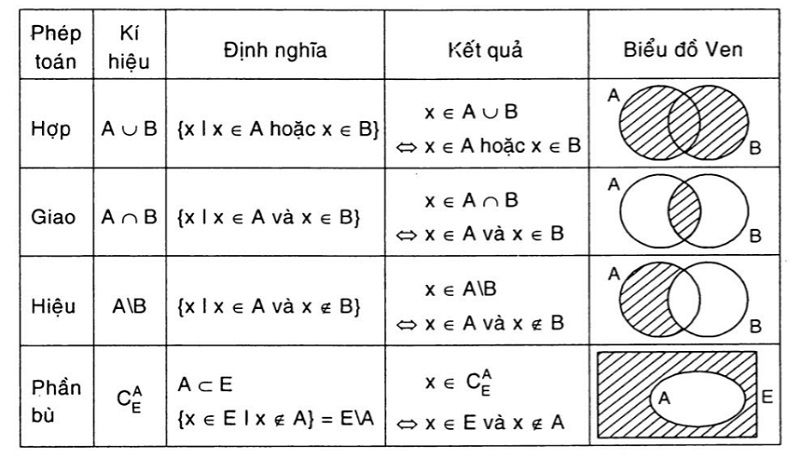
Bài tập xem thêm về tập hợp số
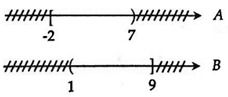
Vậy A ∪ B = <-2;7> ∪ (1;9> = <-2;9> .
Như vậy, với phần đông thông tin hữu dụng trên. Các bạn đã đọc hơn về khái niệm cũng như các chăm đề luân chuyển quanh tập vừa lòng số là gì? Chúc mọi tín đồ học tập thật giỏi và áp dụng kiến thức chính xác trong quy trình học tập của mình.
Các tập hòa hợp số trong toán học sẽ cho chính mình biết được từng nhiều loại với các thông tin đầy đủ. Rộng hết chính là mối quan liêu hệ của những tập hợp kia trong Toán Học.
Với những nội dung dưới nội dung bài viết này, chắc chắn sẽ cho mình thêm các nội dung hữu dụng !
Tham khảo nội dung bài viết khác:
lý thuyết các tập phù hợp số học
1. Tập thích hợp số từ nhiên, kí hiệu N
N = 1; 2; 3; 4; 5…….
2. Tập hợp số nguyên, kí hiệu là Z
Z = … -3; -2; -1; 0; 1; 2; 3……..
– Tập vừa lòng số nguyên tất cả các bộ phận là số thoải mái và tự nhiên và các bộ phận đối của các số từ nhiên.
– Tập hợp các số nguyên dương kí hiệu là N∗
3. Tập vừa lòng số hữu tỉ, kí hiệu là Q
Q = a/b / a, b ∈ Z, b ≠ 0
– từng số hữu tỉ hoàn toàn có thể biểu diễn bằng một số trong những thập phân hữu hạn hoặc vô hạn tuần hoàn.
4. Tập phù hợp số thực, kí hiệu là R
– một trong những được màn biểu diễn bằng một vài thập phân vô hạn ko tuần hoàn được call là một số trong những vô tỉ. Tập hợp các số vô tỉ kí hiệu là I
– Tập hòa hợp số thực gồm những số hữu tỉ và các số vô tỉ:
R = Q ∪ I
5. Mọt quan hệ các tập hợp số
+) Ta tất cả : R = Q ∪ I.
+) Tập N ; Z ; Q ; R.
những phép toán trong tập phù hợp của toán học
Với các phép toán trong tập phù hợp số học bên dưới đây, các bạn sẽ biết được quan hệ của chúng.
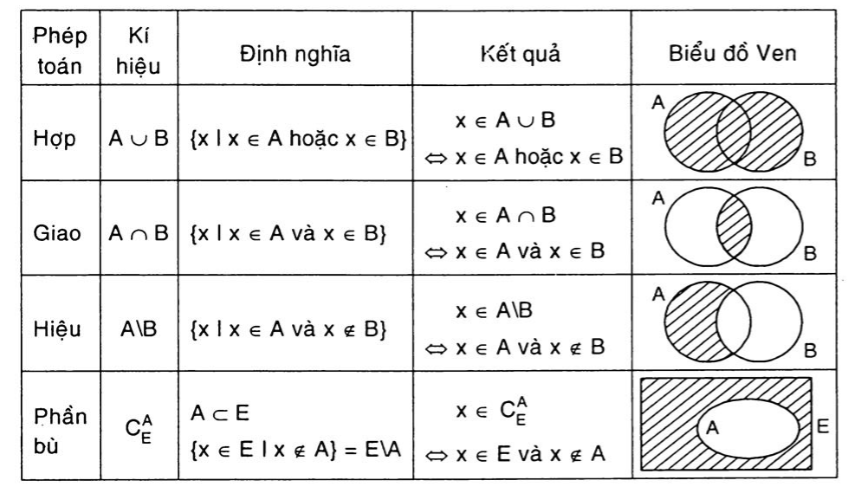
bài xích tập về các tập vừa lòng số học trong Toán
Bài 1: chọn câu vấn đáp đúng trong các câu sau:
a)
Hướng Dẫn Giải:
Chọn câu trả lời D. Vì chưng
Bài 2: khẳng định mỗi tập phù hợp sau:
a) <-2;4)∪(0;5>
b) (-1;6>∩<1;7)
c) (-∞;7)(1;9)
Hướng Dẫn Giải:
a) <-2;4)∪(0;5>=<-2;5>
b) (-1;6>∩<1;7)=<1;6>
c) (-∞;7)(1;9)=(-∞;1>
Đây là dạng toán thường chạm chán nhất, để giải nhanh dạng toán này ta bắt buộc vẽ những tập hợp lên trục số thực trước, phần đem ta vẫn giữa nguyên còn phần không rước ta vẫn gạch bỏ đi. Sau đó việc đem giao, phù hợp hay hiệu sẽ dễ ợt hơn.
Bài 3: xác minh mỗi tập hợp sau
a) (-∞;1>∩(1;2)
b) (-5;7>∩<3;8)
c) (-5;2)∪<-1;4>
d) (-3;2)<0;3>
e) R(-∞;9)
Hướng Dẫn Giải:
a) (-∞;1>∩(1;2) ≠ ∅
b) (-5;7>∩<3;8) = <3;7)
c) (-5;2)∪<-1;4> = (-1;2)
d) (-3;2)<0;3> = (-3;0>
e) R(-∞;9) = <9;+∞)
Cám ơn chúng ta đã theo dõi nội dung bài viết nói về những tập hòa hợp số trong Toán Học tương tự như mối dục tình của chúng. Hy vọng bài viết dưới đây sẽ cho chính mình những nội dung có lợi nhất nhé !









